来自牛津大学和布达佩斯科技与经济大学的数学家团队发现了一种新的形状，可以在不使用尖角的情况下平铺空间。值得注意的是，这些“理想的柔软形状”在自然界中比比皆是——从贝壳到肌肉细胞。
这一发现不仅解释了生物组织的几何形状，而且还可以开启没有角落的新建筑设计。该研究结果已发表在《美国科学院院刊:Nexus》上。
数学家们长期以来一直在研究各种形状如何组合在一起，以覆盖没有缝隙的表面。然而，他们的典型方法——使用尖角和平面的形状——在自然界中很少见到。
相反，生物体使用一系列令人眼花缭乱的模式来形成和生长，例如在肌肉组织中。最引人注目的是，这些图案的特点是具有弯曲的边缘，非平坦的表面，几乎没有尖锐的角。
到目前为止，大自然是如何利用这些“柔软的形状”来实现几何复杂性的，还没有得到数学的解释。
数学家Alain Goriely教授(牛津大学数学研究所)、Gábor Domokos教授、Krisztina Regős教授和Ákos G. Horváth教授(布达佩斯科技与经济大学)发现的答案是一种叫做软细胞的新型数学形状。这些形状有最小数量的尖角，并且覆盖空间没有缝隙。
在二维中，这些软细胞只有两个角的弯曲边界。在肌肉细胞、斑马条纹、河流岛屿的形状、洋葱鳞茎的层，甚至在建筑设计中，都能找到这样的瓷砖图案。
在3D中，这些柔软的细胞变得更加复杂和有趣。该团队首先确定，在3D中，软细胞根本没有角。然后，从传统的3D平铺系统开始，比如立方体网格，团队展示了它们可以通过允许边缘弯曲来软化，同时在这个过程中最小化尖角的数量。通过这样做，他们发现了具有不同平铺特性的全新软细胞类别。
截断八面体的软版本。模特:Krisztina Reg
ő年代。图片:Gábor Domokos。
Gábor多莫科斯教授说:“我们发现，包括扎哈·哈迪德在内的建筑师，只要想避开角落，就会本能地构造出这种形状。”事实上，一群年轻的建筑师利用Gömböc形状的几何形状作为灵感，建造了我们的一个三维软单元。”
这项研究的核心部分是依靠CT图像，展示了标志性鹦鹉螺的内室是没有角的3D软细胞的自然例子。令人惊讶的是，腔室的平面部分是二维软细胞。
阿兰·戈里里教授解释说:“大自然不仅讨厌真空，她似乎也讨厌尖角。”
多莫科斯教授补充说:“软细胞有助于解释为什么当你观察一个腔室壳的横截面时，它会显示出角落，而腔室的三维几何形状却没有。”
软细胞似乎是生物组织的几何构件，它们的存在开启了几何学和生物学的一系列问题。产生软瓷砖的必要条件可以解释为什么某些图案被大自然偏爱。例如，软细胞的概念不仅可以帮助解释组织的静态几何形状，还可以解释尖端生长，这是最普遍的生物形状进化过程之一。
这项名为“软细胞和贝壳几何”的研究发表在《PNAS Nexus》杂志上。
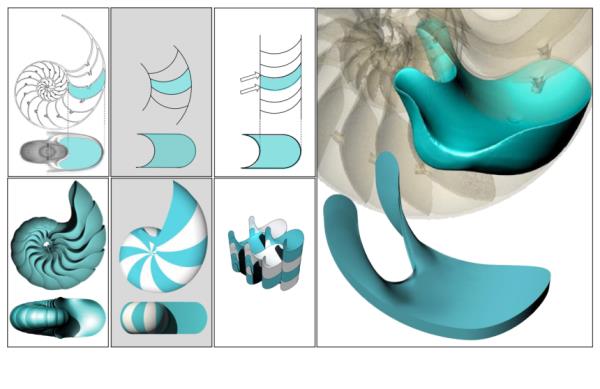软细胞有助于解释为什么当你观察一个腔室壳的横截面时，它会显示出角，而腔室的三维几何形状却没有。图片来源:Krisztina Regõs和Lajos Czegledi。
本文来自作者[易文]投稿，不代表时能五金立场，如若转载，请注明出处：https://xkxky.cn/zsfx/202507-2023.html
评论列表（4条）
我是时能五金的签约作者“易文”！
希望本篇文章《数学家发现生物学中的新普遍形态》能对你有所帮助！
本站[时能五金]内容主要涵盖：国足,欧洲杯,世界杯,篮球,欧冠,亚冠,英超,足球,综合体育
本文概览：来自牛津大学和布达佩斯科技与经济大学的数学家团队发现了一种新的形状，可以在不使用尖角的情况下平铺空间。值得注意的是，这些“理想的柔软形状”在自然界中比比皆是—...